Desert Resonator: Technical Analysis
In this post, I will provide a brief explanation of the signal processing algorithms behind my plug-in, 'Desert Resonator'.
Desert Resonator is a wavetable synthesizer featuring a physical modeling stage, an analog modelling low-pass filter, and a flanger.
This plugin is completely developed using the JUCE framework in C++. I did not utilize any JUCE libraries for the digital signal processing, everything is built from scratch. I incorporated some elements that I previously uploaded on this blog, like the Steiner-Parker filter, which utilizes analog modelling techniques.
At the moment, the code will not be open source, but you can find on my blog the code for some of the stages of this plug-in.
I will explain each of the stages present in this plug-in.
Wavetable Synth
The wavetable is a matrix of 9 different sound samples that are linearly interpolated. In total, the size of the wavetable is 90 samples.
To start, the wavetable is imported into each oscillator. In this scenario, I opted for 6 parallel voices to maintain performance in terms of memory without sacrificing audio quality.
The algorithm for reading the wavetables is relatively simple, an index is incremented based on the frequency of the note. However, this incrementation often results in non-integer values, necessitating the implementation of interpolation to prevent artifacts. In this instance, I have implemented linear interpolation.
A simple envelope with attack, decay, sustain, and release is applied to the wavetable oscillator. Additionally, for each note triggered, a random generator sets the pan of the signal at the moment of rendering. The amount of panning is controlled by the stereo knob. This helps the mono samples of the wavetable achieve a stereo image that is 'mono compatible' since there is no delay between the right and left channels in generating the stereo image.
Physical Modeling. Karplus-Strong Algorithm
In this plug-in, I've implemented a custom version of the Karplus-Strong Algorithm with a low-pass filter cascaded at the output of the delay. The input to this algorithm is the wavetable synthesizer. Below is the original Karplus-Strong block diagram.
The delay is implemented using a circular buffer. By controlling the number of samples (from 10 to 1600 in this case) of delay, you can alter the pitch of the sound. Additionally, adjusting the feedback affects the decay of the sound.
The mix parameter controls the amount of delay applied to the signal. Additionally, linear interpolation is employed to prevent artifacts when modifying the pitch value of the delay samples.
Low Pass Filter. Steiner-Parker Analog Modelling.
This Low Pass Filter is designed using analog modelling techniques. The Steiner-Parker filter is based on the Sallen-Key topology and offers a pleasant resonance sound. I have a blog post that delves into the design of this filter, and the code is also available on my GitHub.
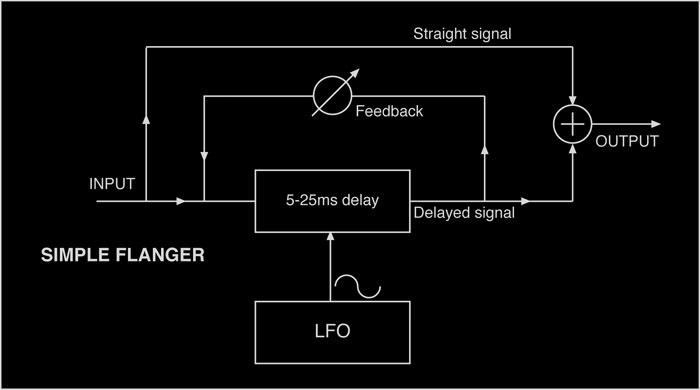
Flanger
The flanger effect is also based on a delay, and its block diagram is similar of the Karplus-Strong algorithm. In my implementation, the delay samples vary between 44 and 244, and they are modulated by a low-frequency sine wave oscillator. Additionally, linear interpolation is used to avoid audio artifacts.
The feedback is crucial, it adds a particular metallic sound that complements the plugin's overall sound tendency.
Output stage and considerations
At the output stage there are just a volume controller and a security limiter to avoid peaks due the nature of the sounds generates by the plug-in.
The movement knob is another LFO that modulates the cutoff and decay parameters of the plugin.
This is a brief explanation of the plugin's algorithms behind the scenes. As you can see, the algorithms themselves are not too complex, but there are numerous considerations in the code, from smoothing parameters to specific modifications. Currently, the code will not be open, but if you are really interested, feel free to reach out to me.
Thank you for reading!