Linkwitz–Riley filters in C++ JUCE for multi-band processing

   

    In this article, you'll learn how to implement a Linkwitz-Riley crossover filter, which is crucial for multiband processing. I'll start with a brief mathematical explanation of the implementation. Then, I'll showcase the equivalent C++ code, and finally, I'll guide you through its application in JUCE for audio processing.

    Through this implementation, you'll not only gain the ability to create a multiband equalizer but also to incorporate your desired processing within each individual band. For example to implement an FX that works by bands.

    Crossover filters are built in terms to get a flat frequency response. These are widely used in audio applications.Each band is constructed using a combination of low-pass and high-pass filters, each composed of two cascaded 2nd order Butterworth filters. Thus, the implementation of each Linkwitz-Riley filter requires the utilization of four Butterworth filters. 

    Using two butterworths in cascade allows us to reduce another 3dB at the cutoff frequency ( -6dB total ) , which means that the total sum with another filter in the same frequency is equal to zero.

    To implement the 2nd order Butterworth filters in the digital domain, we'll employ Biquad Filters, a type of Infinite Impulse Response filter. These filters will be specifically implemented using the direct form 1 configuration. 

C++ implementation

We must implement in code the following equation.

\[ y[n]= (\frac{b_{0}}{a_{0}})x[n] + (\frac{b_{1}}{a_{0}})x[n-1] + (\frac{b_{2}}{a_{0}})x[n-2] - (\frac{a_{1}}{a_{0}})y[n-1] - (\frac{a_{2}}{a_{0}})y[n-2] \]

    To calculate the coefficients of this filter a1, a0, b0, b1 and b2 we will use the following equations. If you are interested in seeing how they are deduced mathematically, I invite you to visit the following post 

For Low pass:

\(b_{0}= \frac{1-cosw_{0}}{2}\)    \(b_{1}= 1-cosw_{0}\)    \(b_{2}= \frac{1-cosw_{0}}{2}\)    

\(a_{0}= 1 + \alpha \)     \(a_{1}= -2cosw_{0}\)      \(a_{2}= 1 - \alpha \) 

For High pass:

\(b_{0}= \frac{1+cosw_{0}}{2}\)    \(b_{1}= -{1-cosw_{0}}\)    \(b_{2}= \frac{1+cosw_{0}}{2}\)    

\(a_{0}= 1 + \alpha \)     \(a_{1}= -2cosw_{0}\)      \(a_{2}= 1 - \alpha \) 

For both:

\(\alpha= \frac{sinw_{0}}{2Q}\)    \(w_{0} = 2\pi\frac{f_{0}}{F_{s}}\)

    Regarding the code, a class named "Biquad" is established (located at Source/BiquadFilter.cpp), featuring the member function "processbiquadbp", which encapsulates the filter implementation.

    On my GitHub repository, you'll observe that I've additionally crafted the functions HP (exclusive high-pass filter) and LP (exclusive low-pass filter).

    Those filters are situated at the band's endpoints because employing band-pass filters at these junctures lacks practical significance.

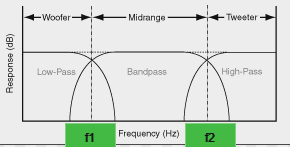
    This is a demonstrative graphic with the names that I used for each frequency. 

    For the JUCE implementation we need to create a new buffer for each band in the process block. On output, add all buffers. Here, an explanation of the code and where to add your process for each band.

void MultibandCrossoverAudioProcessor::processBlock (juce::AudioBuffer<float>& buffer, juce::MidiBuffer& midiMessages)
{
    juce::ScopedNoDenormals noDenormals;
    auto totalNumInputChannels = getTotalNumInputChannels();
    auto totalNumOutputChannels = getTotalNumOutputChannels();


    for (auto i = totalNumInputChannels; i < totalNumOutputChannels; ++i)
        buffer.clear(i, 0, buffer.getNumSamples());

    //create a new buffer for each filter

    juce::AudioBuffer<float> band1Buffer(totalNumInputChannels, buffer.getNumSamples());
    juce::AudioBuffer<float> band2Buffer(totalNumInputChannels, buffer.getNumSamples());
    juce::AudioBuffer<float> band3Buffer(totalNumInputChannels, buffer.getNumSamples());
    band1Buffer.clear();
    band2Buffer.clear();
    band3Buffer.clear();


    for (int channel = 0; channel < totalNumInputChannels; ++channel)
    {
        auto* channelData = buffer.getWritePointer(channel);

        //band 1 
        ptrBiquad1[channel]->processBiquadLP(channelData, band1Buffer.getWritePointer(channel), buffer.getNumSamples(), getSampleRate(), *parameters.getRawParameterValue("f1"), *parameters.getRawParameterValue("BAND1_gain_ID")); 
		
        // Here add process for band 1
        
        //band 2 
        ptrBiquad2[channel]->processBiquadBP(channelData, band2Buffer.getWritePointer(channel), buffer.getNumSamples(), getSampleRate(), *parameters.getRawParameterValue("f1"), *parameters.getRawParameterValue("f2"), *parameters.getRawParameterValue("BAND2_gain_ID"));

        // Here add process for band 2
        
        //band 3 
        ptrBiquad3[channel]->processBiquadHP(channelData, band3Buffer.getWritePointer(channel), buffer.getNumSamples(), getSampleRate(), *parameters.getRawParameterValue("f2"), *parameters.getRawParameterValue("BAND3_gain_ID"));
        
        // Here add process for band 3
        
    }
        
    // sum of three filters

    for (int channel = 0; channel < totalNumInputChannels; ++channel)
    {
        auto* channelData = buffer.getWritePointer(channel);

        auto* band1Data = band1Buffer.getReadPointer(channel);
        auto* band2Data = band2Buffer.getReadPointer(channel);
        auto* band3Data = band3Buffer.getReadPointer(channel);

        for (int sample = 0; sample < buffer.getNumSamples(); ++sample)
        {
            channelData[sample] = band1Data[sample] + band2Data[sample] + band3Data[sample];
        }
    }
}

    Thank you for reading!